
How well do Patterson's sequential and parallel methods of computing the quantity π/4 perform? Recall that the sequential method was to sum the infinite series for arctangent of one radian, while the parallel method was to compute the probability of a point falling within a unit circle when that point was randomly chosen from the square enclosing the unit circle.
To evaluate the sequential algorithm, let's look at its rate of convergence:
| Iteration | π/4 | π | Error |
|---|---|---|---|
| 0 | 1.0000 | 4.0000 | 0.8584 |
| 1 | 0.6667 | 2.6667 | -0.4749 |
| 2 | 0.8667 | 3.4667 | 0.3251 |
| 3 | 0.7238 | 2.8952 | -0.2464 |
| 4 | 0.8349 | 3.3397 | 0.1981 |
| 5 | 0.7440 | 2.9760 | -0.1655 |
| 6 | 0.8209 | 3.2837 | 0.1421 |
| 7 | 0.7543 | 3.0171 | -0.1245 |
| 8 | 0.8131 | 3.2524 | 0.1108 |
| 9 | 0.7605 | 3.0418 | -0.0998 |
| 10 | 0.8081 | 3.2323 | 0.0907 |
This rate of convergence is painfully slow: after ten iterations, we do not yet have even two decimal digits of π. A few centuries ago, John Machin derived a much faster series for π/4 based on the following formula:

Machin's series accumulates about 1.5 decimal digits per iteration:
| Iteration | π/4 | π | Error |
|---|---|---|---|
| 0 | .795815899581589958 | 3.18326359832635983 | .04167094473656659 |
| 1 | .785149257331515078 | 3.14059702932606031 | -.00099562426373292 |
| 2 | .785405257331258606 | 3.1416210293250344 | .00002837573524118 |
| 3 | .785397943045544323 | 3.14159177218217729 | -.00000088140761594 |
| 4 | .785398170601099879 | 3.14159268240439951 | .00000002881460627 |
| 5 | .785398163153827152 | 3.14159265261530860 | -.00000000097448463 |
| 6 | .785398163405888690 | 3.14159265362355476 | .00000000003376152 |
| 7 | .785398163397150557 | 3.14159265358860222 | -.00000000000119100 |
| 8 | .785398163397458961 | 3.14159265358983584 | .00000000000004260 |
| 9 | .785398163397447924 | 3.14159265358979169 | -.00000000000000154 |
| 10 | .785398163397448323 | 3.14159265358979329 | .00000000000000005 |
So Patterson's choice of series for π/4 falls a bit short of recent practice, to say the least.
But what of his Monte Carlo parallel method? One can clearly build a good parallel program on it by having each of N tasks compute 1/N of the desired number of trials, and then combining their results. Increasing the desired number of trials will drive the parallel communication overhead down to an arbitrarily low level. So scalability of Patterson's Monte Carlo method is nothing short of excellent.
But scalability is only part of the problem to be solved. Raw performance is also critically important.
To analyze this method's performance, consider that the first trial will either be within the unit circle (which gives the estimate π=4) or outside of it (which gives the estimate π=0). The second trial adds the possibility of the estimate π=2. After ten trials, we might possibly have an estimate as good as π=3, or one digit. After one hundred trials, we might (or might not) have an estimate as good as π=3.1.
Continuing this line of thought:
| Number of Trials | Maximum Possible Correct Digits of π |
|---|---|
| 1 | 0 |
| 10 | 1 |
| 100 | 2 |
| 1000 | 3 |
| 10,000 | 4 |
| 100,000 | 5 |
| 1,000,000 | 6 |
| 10,000,000 | 7 |
| 100,000,000 | 8 |
| 1,000,000,000 | 9 |
| 10,000,000,000 | 10 |
| 100,000,000,000 | 11 |
| 1,000,000,000,000 | 12 |
| 10,000,000,000,000 | 13 |
| 100,000,000,000,000 | 14 |
| 1,000,000,000,000,000 | 15 |
Attaining the 15-digit accuracy that Machin's formula delivered after
only 10 iterations thus requires at least one quadrillion trials.
Therefore, if we had a 1,000-CPU system that could do one trial per
nanosecond, it would take more than 15 minutes to compute π to
at most 15 places.
In contrast, my laptop system took 20 milliseconds to compute this
same accuracy using Machin's formula, even with the performance
penalty imposed by the bc interpretor.
In short, when doing mathematics with parallel computers, you
need not only good parallel design, but also good mathematics.
Patterson's approach scores quite highly in the parallel-design
department, but falls short in the good-mathematics department.
That said, Machin lived centuries ago. What is the state of the art of computing π in 2010?
As of this writing, the effort that has computed the most digits of π on a desktop system used y-cruncher, which, for the record, is a parallel program. The Chudnovsky formula, which delivers 14 decimal digits per iteration, and is based on earlier work by Ramanujan, was used for the computation.
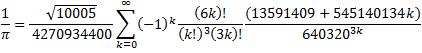
So, once again, attaining good performance and scalability requires not just good parallel design, but also good mathematics.